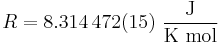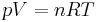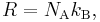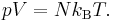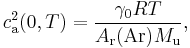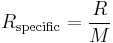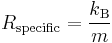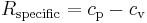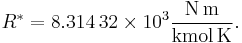Gas constant

Values of R ^[1]	Units (V P T ⁻¹ n⁻¹)
8.314472(15)	J K⁻¹ mol⁻¹
1.9858775(34)	cal K⁻¹ mol⁻¹
8.314472(15)×10⁷	erg K⁻¹ mol⁻¹
8.314472(15)	L kPa K⁻¹ mol⁻¹
8.314472(15)	m³ Pa K⁻¹ mol⁻¹
8.314472(15)	cm³ MPa K⁻¹ mol⁻¹
8.314472×10⁻⁵	m³ bar K⁻¹ mol⁻¹
8.205746×10⁻⁵	m³ atm K⁻¹ mol⁻¹
82.05746	cm³ atm K⁻¹ mol⁻¹
84.78402×10⁻⁶	m³ kgf/cm² K⁻¹ mol⁻¹
8.314472×10⁻²	L bar K⁻¹ mol⁻¹
0.08205746(14)	L atm K⁻¹ mol⁻¹
62.36367(11)	L mmHg K⁻¹ mol⁻¹
62.36367(11)	L Torr K⁻¹ mol⁻¹
6.132440(10)	ft lbf K⁻¹ g-mol⁻¹
1,545.349(3)	ft lbf °R⁻¹ lb-mol⁻¹
10.73159(2)	ft³ psi °R⁻¹ lb-mol⁻¹
0.7302413(12)	ft³ atm °R⁻¹ lb-mol⁻¹
998.9701(17)	ft³ mmHg K⁻¹ lb-mol⁻¹
1.986	Btu lb-mol⁻¹ °R⁻¹

The gas constant (also known as the molar, universal, or ideal gas constant, denoted by the symbol R or R) is a physical constant which is featured in a large number of fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy (i.e. the pressure-volume product) per kelvin per mole (rather than energy per kelvin per particle).

Its value is

$R=8.314\,472(15)~\frac{\mathrm{J}}{\mathrm{K~mol}}$

The two digits in parentheses are the uncertainty (standard deviation) in the last two digits of the value. The relative uncertainty is 1.8 × 10⁻⁶.

The gas constant occurs in the ideal gas law, as follows:

$pV = nRT\,\!$

where p is the absolute pressure, V is the volume of gas, n is the number of moles of gas, and T is thermodynamic temperature. The gas constant has the same units as molar entropy.

1 Relationship with the Boltzmann constant
2 Measurement
3 Specific gas constant
4 U.S. Standard Atmosphere
5 See also
6 References

Relationship with the Boltzmann constant

The Boltzmann constant k_B (often abbreviated k) may be used in place of the gas constant by working in pure particle count, N, rather than number of moles, n, since

$\qquad R = N_{\rm A} k_{\rm B},\,$

where N_A is the Avogadro constant. For example, the ideal gas law in terms of Boltzmann's constant is

$pV = N k_{\rm B} T.\,\!$

Measurement

As of 2006, the most precise measurement of R is obtained by measuring the speed of sound c_a(p, T) in argon at the temperature T of the triple point of water (used to define the kelvin) at different pressures p, and extrapolating to the zero-pressure limit c_a(0, T). The value of R is then obtained from the relation

$c_\mathrm{a}^2(0, T) = \frac{\gamma_0 R T}{A_\mathrm{r}(\mathrm{Ar}) M_\mathrm{u}},$

where:

γ₀ is the heat capacity ratio (5/3 for monatomic gases such as argon);
T is the temperature, T_TPW = 273.16 K by definition of the kelvin;
A_r(Ar) is the relative atomic mass of argon and M_u = 10⁻³ kg mol⁻¹.^[1]

Specific gas constant

R_specific for dry air	Units
287.058	J kg⁻¹ K⁻¹
53.3533	ft lbf lb⁻¹ °R⁻¹
1716.59	ft lbf slug⁻¹ °R⁻¹
Based on a mean molar mass for dry air of 28.9645 g/mol.

The specific gas constant of a gas or a mixture of gases (R_specific) is given by the molar gas constant, divided by the molar mass (M) of the gas/mixture.

$R_{\rm specific} = \frac{R}{M}$

Just as the ideal gas constant can be related to the Boltzmann constant, so can the specific gas constant by dividing the Boltzmann constant by the molecular mass of the gas.

$R_{\rm specific} = \frac{k_{\rm B}}{m}$

Another important relationship comes from thermodynamics. This relates the specific gas constant to the specific heats for a calorically perfect gas and a thermally perfect gas.

$R_{\rm specific} = c_{\rm p} - c_{\rm v}\$

where c_p is the specific heat for a constant pressure and c_v is the specific heat for a constant volume.^[2]

It is common, especially in engineering applications, to represent the specific gas constant by the symbol R. In such cases, the universal gas constant is usually given a different symbol such as R to distinguish it. In any case, the context and/or units of the gas constant should make it clear as to whether the universal or specific gas constant is being referred to.^[3]

U.S. Standard Atmosphere

The U.S. Standard Atmosphere, 1976 (USSA1976) defines the gas constant R* as:^[4]^[5]

$R^* = 8.314\,32\times 10^3 \frac{\mathrm{N\,m}}{\mathrm{kmol\,K}}.$

The USSA1976 does recognize, however, that this value is not consistent with the cited values for the Avogadro constant and the Boltzmann constant.^[5] This disparity is not a significant departure from accuracy, and USSA1976 uses this value of R* for all the calculations of the standard atmosphere. When using the ISO value of R, the calculated pressure increases by only 0.62 pascal at 11 kilometers (the equivalent of a difference of only 0.174 meter or 6.8 inches) and an increase of 0.292 Pa at 20 km (the equivalent of a difference of only 0.338 m or 13.2 in).

References

↑ ^1.0 ^1.1 Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006". Rev. Mod. Phys. 80: 633–730. doi:10.1103/RevModPhys.80.633. http://physics.nist.gov/cuu/Constants/codata.pdf. Direct link to value.
↑ Anderson, Hypersonic and High-Temperature Gas Dynamics, AIAA Education Series, 2nd Ed, 2006
↑ Moran and Shapiro, Fundamentals of Engineering Thermodynamics, Wiley, 4th Ed, 2000
↑ "Standard Atmospheres". http://www.sworld.com.au/steven/space/atmosphere/. Retrieved 2007-01-07.
↑ ^5.0 ^5.1 U.S. Standard Atmosphere, 1976, U.S. Government Printing Office, Washington, D.C., 1976 (Linked file is 17 MiB).